Ein Halbquadrat wird als Halbquadrat bezeichnet, weil man es erzeugen kann, indem man ein Quadrat über seine Diagonale teilt. Dieser Artikel beschreibt, wie man ein solches Halbquadrat aus einem RegularPolygon erstellt. Dabei soll das Halbquadrat in einem quadratischen Canvas-Steuerelement platziert werden und zwar exakt so, dass es das Canvas über seine Diagonale teilt. Außerdem soll das Halbquadrat auch dann, wenn es einen Rand hat, also eine StrokeThickness mit einem Wert größer als "0", jeweils exakt positioniert bleiben. Das ist etwas trickreich. Schließlich soll das Halbquadrat so konfiguriert werden, dass es nur über eine einzige Eigenschaftsänderung ("Rotation") die Eck-Ausrichtung des rechten Winkels ändert.
Auf geht's.
Vorbemerkung
Ein RegularPolygon wird in "Expression Blend" als Triangle (Dreieck) bezeichnet. Im folgenden werde ich nur die Bezeichnung "Triangle" (Dreieck) verwenden, weil ein Triangle ein RegularPolygon ist, das über drei Punkte definiert wird.
Ein bißchen Geometrie
Gegeben ist ein Quadrat. Das Quadrat hat bekanntlich vier gleichlange Seiten. Die Seitenlänge des Quadrats wird mit "a" bezeichnet. Die Diagonale, die das Quadrat teilt, wird mit "d" bezeichnet. Die folgende Skizze visualisiert das:
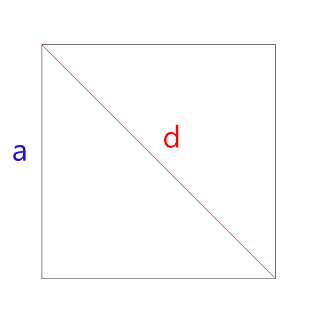
Die Länge der Diagonalen "d" wird wie folgt berechnet:
d = √ 2 * a
Beispielrechnung:
a = 100
d = ?
d = 1.4142135623730950488016887242097 * 100
d = 141.42135623730950488016887242097
Die Höhe des Halbquadrats ist gleich der Hälfte der Diagonalen "d", also:
h = d * 0.5
Mehr Mathematik wird zunächst nicht benötigt, um zu verstehen, wie ein Halbquadrat geometrisch berechnet wird.
Trotzdem möchte ich an dieser Stelle bereits auf einen wichtigen Punkt hinweisen. Die Übertragung dieser geometrischen Berechnungsformel auf ein Dreieck, das in einer Silverlight-Anwendung verwendet werden soll, funktioniert nur eingeschränkt. Eingeschränkt insofern, als dass es zwar für ein Dreieck ohne Rand, nicht jedoch für ein Dreieck mit Rand funktioniert. Um das Problem zu verdeutlichen, verwende ich im folgenden Beispiel trotzdem zunächst diese reine geometrische Formel. Im weiteren Verlauf stelle ich dann die Formeln vor, die benötigt werden, um ein Dreieck mit Rand als Halbquadrat verwenden zu können.
Ein bißchen Blend
Um die Vorgehensweise zu verdeutlichen, wird ein Beispielprojekt erstellt. Der Oberfläche wird ein quadratisches Canvas hinzugefügt. Die Werte für Breite und Höhe betragen jeweils "150":
Mit einem Doppelklick auf die Form "Triangle" wird dem selektierten Canvas ein "Triangle"-Element hinzugefügt:
Der Wert für "StrokeThickness" wird zunächst auf "0" gesetzt. Ich gehe etwas später darauf ein, wie man die Berechnung der Größe des Halbquadrats modifizieren muss, um auch mit einer "StrokeThickness" > "0" das Halbquadrat so zu erzeugen, dass es exakt in das quadratische Canvas paßt.
Das Halbquadrat soll so im Canvas platziert werden, dass seine Breite der Länge der Diagonalen des Canvas entspricht. Deswegen wird anhand der oben genannten Formel die Breite des Halbquadrats berechnet. Die Seitenlänge des Canvas beträgt 150px. Also hat "a" den Wert 150. Die Berechnung lautet also:
d = 1.4142135623730950488016887242097 * 150
d = 212.132
Der Wert von "d" wird als Breite des Triangle eingetragen. Die Höhe des Triangle ist gleich der Hälfte der Länge der Diagonalen:
Danach sieht das Triangel so aus:
Wenn das Triangle jetzt um 45° gedreht wird, werden die gleichlangen Schenkel, die zueinander im rechten Winkel stehen, so ausgerichtet, dass sie parallel zu den Seiten des quadratischen Canvas verlaufen:
Das Triangle sieht dann so aus:
Das obige Bild zeigt, dass das Dreieck jetzt einen leichten Versatz hat. Es ist leicht nach links und nach unten versetzt. Diesen Versatz müssen wir beseitigen. Um diesen Versatz zu beseitigen, wird eine Translation über die X-Achse und über die Y-Achse benutzt. Für ein Triangle, das einen Wert für "StrokeThickness" = "0" hat, kann man folgende Formel benutzen, um die Werte für die Translations-Transformationen zu berechnen:
TranslateX = ((d - a) : 2) * -1
TranslateY = ((d - a) : 2) * -1
Damit diese Formel funktioniert, müssen die Werte für "RenderTransformOrigin" des "Triangle" folgendermaßen eingestellt werden:
Mit diesen Werten wird der Drehmittelpunkt des "Triangle" genau in der Mitte seines unteren Randes positioniert.
Jetzt wird die Formel angewendet ...
TranslateX = ((212.132 - 150) : 2) * -1
TranslateX = 31.066
TranslateY = ((212.132 - 150) : 2) * -1
TranslateY = 31.066
... und die Berechnungsergebnisse als X- bzw. Y-Translation des Triangle zugewiesen:
Jetzt sieht das Triangle innerhalb des Canvas folgendermaßen aus:
Aber halt. Nicht zu früh freuen! Denn bisher hat das Triangle eine "StrokeThickness" mit dem Wert "0". Was passiert, wenn wir dem "Triangle" jetzt eine "StrokeThickness" mit einem Wert > 0 zuweisen? Es passiert das hier, bei einer "StrokeThickness" mit einem Wert von beispielsweise "30":
Im obigen Bild hat der Stroke die Farbe blau. Man sieht, dass das Dreiecks offensichtlich seine exakte Positionierung verloren hat und das Dreieck ist auch kein gleichschenklig-rechtwinkliges Dreieck mehr. Um dieses ungewünschte Ergebnis zu bereinigen, müssen die Formeln zur Berechnung der Werte des Triangle folgendermaßen geändert werden, wobei "s" der Wert für die StrokeThickness ist:
a = 150
d = √ 2 * (a - s)
Triangle Width = d
d = √ 2 * (a - s)
d = √ 2 * (150 - 30)
=> Triangle Width = 169.7056
Triangle Height = h
h = (d : 2) + (s * 0.5)
h = (169.7056 : 2) + (30 * 0.5)
h = 99.8528
=> Triangle Height = 99.8528
TranslateX = ((d - a) * 0.5) * -1
TranslateX = ((169.7056 - 150) * 0.5) * -1
=> TranslateX = -9.8528
TranslateY = (((d - a) * 0.5) + (s * 0.5)) * -1
TranslateY = (((169.7056 - 150) * 0.5) + (30 * 0.5)) * -1
=> TranslateY = -24.8528
Zur Probe werden die obigen Berechnungsergebnisse als Eigenschaftswerte für das Triangle eingetragen:
Das Dreieck sieht nach diesen Änderungen so aus, wie es aussehen soll. Es fügt sich wieder exakt in das quadratische Canvas ein:
Änderung der Ausrichtung
Ich hatte weiter oben den Drehmittelpunkt des Dreiecks in der Mitte seines unteren Randes positioniert. Zur Erinnerung: Das erfolgte über die Einstellungen von RenderTransformOrigin. Der Vorteil des so definierten Drehmittelpunktes ist, dass das Dreieck jetzt sehr einfach in seiner Ausrichtung verändert werden kann. Und zwar über den Wert für die Rotation. Gegenwärtig beträgt der Drehwinkel 45°. Damit zeigt das Dreieck mit seinem rechten Winkel nach oben rechts. Über die Veränderung des Rotationswinkels kann die Ausrichtung verändert werden:
Rotation ----- Ausrichtung
-45° oben links
45 oben rechts
135 unten rechts
-135 unten links
Ein Berechnungsprogramm als Helfer
Ich habe ein kleines Berechnungsprogramm erstellt, das die erforderlichen Werte für ein Halbquadrat vornimmt. Hier ist es, die Bedienung sollte selbsterklärend sein:
Das Berechnungsprogramms kann einschließlich Quellcode in der Expression Gallery heruntergeladen werden.
Download: Quellcode des Berechnungsprogramms.
Viel Spaß also beim Design mit Halbquadraten.















Keine Kommentare:
Kommentar veröffentlichen